Introduction : Pourquoi viser un pylône électrique ?

En astrophotographie, on parle souvent de “pouvoir de résolution” et de “secondes d’arc”, mais ces termes restent souvent abstraits. Avant de pointer mon Flextube 400p vers les planètes, j’ai voulu réaliser un test concret, ici sur Terre, pour visualiser ce que mon instrument a vraiment dans le ventre.

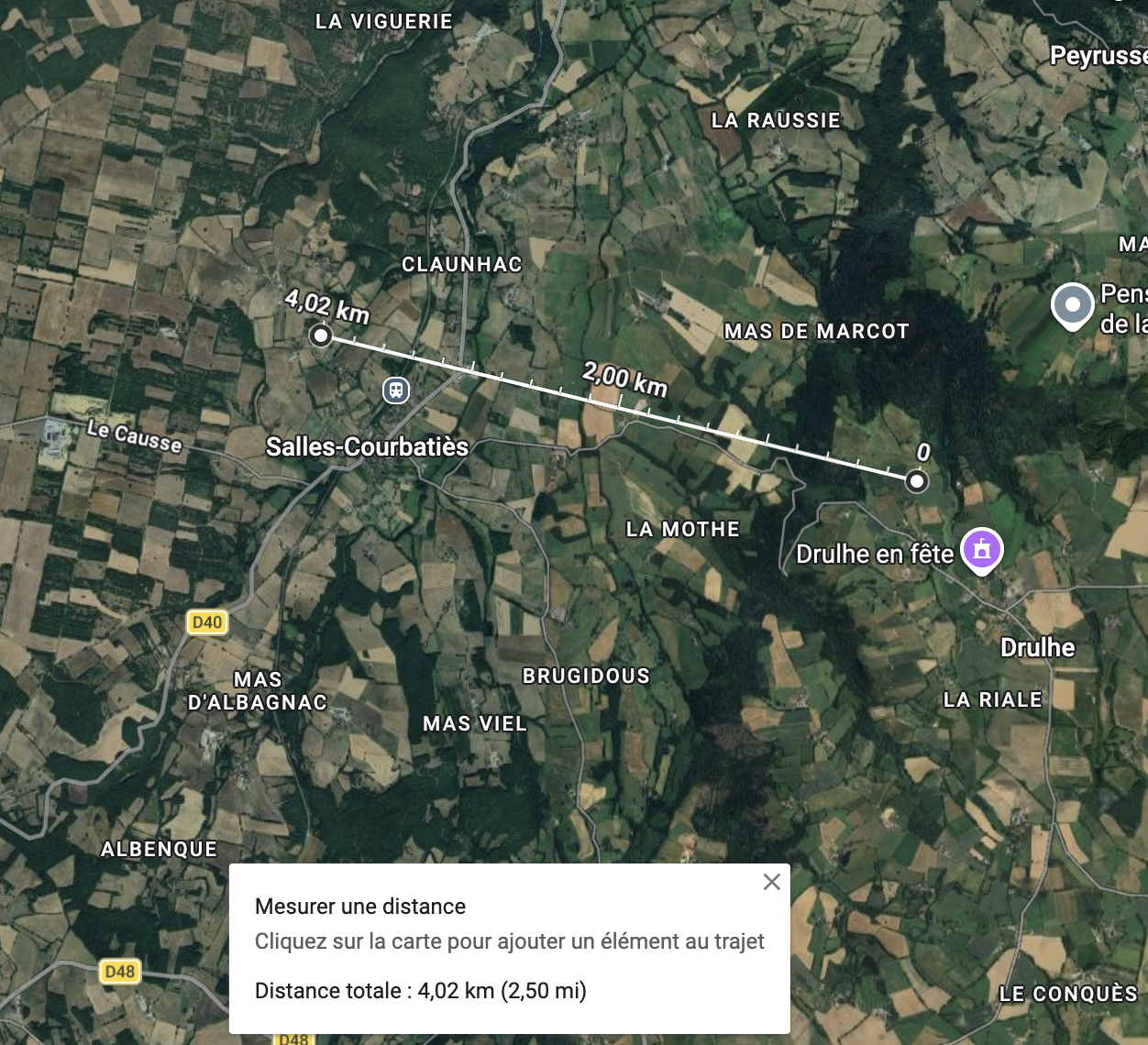
J’ai choisi une cible impitoyable : une ligne à haute tension située à 4,02 km de mon point d’observation (vérifié sur Google Maps). Mon but ? Voir si je pouvais résoudre les détails des isolateurs en verre. Le résultat dépasse mes espérances et offre un comparatif fascinant avec l’observation de Jupiter.

Voici la recherche google de mon fameux pylône bien visible sur Street View !!!!

Voici la vue du pylône à 4,02km de distance. Il est immense mais vu de ci-loin c’est terriblement minuscule !!!

Le Setup et la Cible

• Instrument : Dobson Flextube 400p (400 mm de diamètre). “Voir mon Article sur l’upgrade du train optique”
• Caméra : ASI585MC.
• Barlow : Powermate Televue 2″ (4x)
• La cible : Un isolateur de ligne 400 000 Volts.
• Distance : 4020 mètres.
• Traitement : Stacking vidéo (.ser) avec AutoStakkert! et traitement des ondelettes avec Astrosurface.

Et enfin le résultat à 4km de distance !!!

L’image que vous voyez ci-dessous n’est pas une simple photo, mais un empilement de centaines d’images vidéo pour figer la turbulence atmosphérique, exactement comme on le fait pour Mars ou Saturne.

Comprendre la taille : Du Degré à la Seconde d’arc

Pour comprendre la performance, il faut faire un peu de géométrie, mais promis, on reste simple !

En astronomie, on ne mesure pas les objets en mètres, mais en angles. L’unité de base est le degré (°).

• Le ciel complet fait 360°.
• La Pleine Lune fait environ 0,5°.
• Mon petit doigt, bras tendu, cache environ 1°.

Mais pour les détails fins, le degré est immense. On le découpe donc comme une horloge :

1. Un degré = 60 minutes d’arc.
2. Une minute = 60 secondes d’arc (“). Donc, 1 degré = 3600 secondes d’arc.

Le calcul de ma photo

L’objet que j’ai photographié (la coupelle verte de l’isolateur) mesure environ 25 cm de diamètre. Il est situé à 4020 mètres.

Pour les plus curieux d’entre vous, voici comment nous sommes passés des mètres aux degrés, puis aux secondes d’arc. Rassurez-vous, c’est de la trigonométrie très simple !

Imaginez un immense triangle isocèle très pointu.

• La base du triangle est notre objet (l’isolateur) : 0,25 m.
• La hauteur du triangle est la distance qui nous sépare de l’objet : 4020 m.
• L’angle au sommet est ce que nous cherchons (la taille apparente).

Étape 1 : Le calcul en Radians (L’approximation des petits angles)

En astronomie, quand un objet est très lointain, on n’a pas besoin de formules compliquées. On utilise une règle simple : l’angle est égal à la taille divisée par la distance.

Le résultat de cette division nous donne l’angle dans une unité mathématique brute appelée le Radian.

$$Angle_{(rad)} = \frac{\text{Taille de l’objet}}{\text{Distance}}$$

$$Angle_{(rad)} = \frac{0,25}{4020} = \mathbf{0,00006219 \text{ rad}}$$

Étape 2 : La conversion en Degrés

Le radian c’est bien pour les calculatrices, mais ça ne nous parle pas. Pour convertir des radians en degrés, on multiplie par 57,3 (car $1 \text{ radian} = \frac{180}{\pi} \approx 57,296^\circ$).

$$Angle_{(deg)} = 0,00006219 \times 57,296 \approx \mathbf{0,00356^{\circ}}$$

C’est ainsi que nous obtenons ce fameux chiffre de 0,0035°.

Étape 3 : Le passage aux Secondes d’arc

Comme 0,0035° est un chiffre difficile à manipuler, on le convertit en secondes d’arc (l’unité de précision des astronomes).

Sachant qu’il y a 3600 secondes dans 1 degré :

$$0,00356^{\circ} \times 3600 = \mathbf{12,8″}$$

Résultat : Cet isolateur à 4 km a une taille apparente d’environ 13 secondes d’arc.

Le comparatif : L’isolateur vs Jupiter

C’est là que ça devient intéressant. À quoi correspondent 13 secondes d’arc dans le ciel nocturne ?

• Jupiter : Selon sa distance à la Terre, la géante gazeuse mesure entre 30″ et 50″.
• Mon isolateur : Il mesure 13″.

Cela signifie que si je collais cet isolateur dans le ciel à côté de Jupiter, il serait environ 3 fois plus petit que la planète !

Mais regardez les détails sur mon image : on distingue l’espace entre les coupelles de verre. Cet espace mesure à peine 2 ou 3 cm en réalité. À 4 km de distance, cet espace représente environ 1 seconde d’arc.

1 seconde d’arc, c’est :

• La taille d’une pièce de 1 euro vue à 4 km.
• La taille des ovales blancs ou des détails dans la Grande Tache Rouge sur Jupiter.

Et demain ? Le saut dans l’hyper-résolution avec l’ELT

Si mon Dobson de 400 mm vous semble imposant et que résoudre un détail d’une seconde d’arc à travers l’atmosphère est une belle prouesse, préparez-vous à avoir le vertige.

Actuellement en construction dans le désert d’Atacama au Chili, l’ELT (Extremely Large Telescope) de l’Observatoire Européen Austral (ESO) sera le plus grand œil jamais tourné vers le ciel.

Le combat des diamètres

La résolution d’un télescope dépend avant tout de son diamètre. Comparons :

• Mon Flextube 400p : Un miroir primaire de 0,4 mètre.
• L’ELT : Un miroir primaire segmenté de 39 mètres de diamètre.

L’ELT est presque 100 fois plus large que mon télescope. Sa surface collectrice de lumière est près de 10 000 fois supérieure.

Vaincre l’atmosphère : L’Optique Adaptative

Sur mon image du pylône, j’ai dû utiliser la technique du “stacking” vidéo pour figer la turbulence de l’air. Malgré cela, ma résolution reste limitée par l’atmosphère (le “seeing”).

L’ELT, lui, triche. Il utilisera une technologie de pointe : l’optique adaptative. Des lasers créent de fausses étoiles dans le ciel, des capteurs analysent la turbulence en temps réel, et des miroirs déformables corrigent l’image des milliers de fois par seconde. L’ELT verra le ciel depuis le sol presque aussi nettement que s’il était dans l’espace.

Le comparatif final sur notre pylône

Revenons à notre isolateur situé à 4,02 km.

• Avec mon 400mm : Je parviens à distinguer des détails d’environ 2 à 3 cm (l’espace entre les coupelles ou les tiges de fixation). C’est une résolution d’environ 1 seconde d’arc.
• Avec l’ELT (théorique) : Grâce à son diamètre immense et son optique adaptative, l’ELT vise une résolution dans le visible d’environ 4 millièmes de seconde d’arc (0,004″).

C’est une résolution 250 fois supérieure à celle de mon image !

Si l’ELT pouvait pointer à l’horizontale vers ce même pylône à 4 km, il ne verrait pas juste les vis… Il pourrait distinguer un cheveu humain posé sur l’isolateur.

Pourquoi une telle puissance ?

Les astronomes n’utiliseront évidemment pas l’ELT pour regarder des lignes électriques. Cette résolution insensée servira à :

1. Voir des détails sur la surface des lunes glacées de Jupiter et Saturne.
2. Observer les toutes premières galaxies nées après le Big Bang.
3. Et surtout, tenter de photographier directement des exoplanètes rocheuses de la taille de la Terre autour d’autres étoiles, et peut-être analyser leur atmosphère pour y chercher des traces de vie.

Mon 400mm m’ouvre les portes du système solaire ; l’ELT nous ouvrira les portes de l’Univers lointain.

Le défi de la pièce de 1 Euro : 400mm vs ELT

Pour bien se rendre compte du saut technologique, imaginons un défi simple : lire “pile ou face” sur une pièce de 1 euro (2,3 cm de diamètre).

• Avec mon Dobson 400mm : Je peux distinguer la pièce à environ 4 km de distance. C’est déjà la distance entre le centre d’une ville et sa banlieue !
• Avec l’ELT (Extremely Large Telescope) : Grâce à son miroir de 39 mètres, l’ELT pourrait théoriquement distinguer cette même pièce de monnaie à 1 200 km de distance.

1 200 km, c’est quoi ? Cela signifie que si l’ELT était installé au sommet de la Tour Eiffel à Paris, il pourrait voir une pièce de 1 euro posée sur le Colisée à Rome, ou sur la Puerta del Sol à Madrid.

C’est cette précision chirurgicale qui permettra aux astronomes de traquer des exoplanètes de la taille de la Terre situées à des dizaines de milliers de milliards de kilomètres de nous.

Conclusion

Ce test terrestre prouve que le Flextube 400p est capable de résoudre des détails de l’ordre de la seconde d’arc, même à travers les couches basses et turbulentes de l’atmosphère terrestre.

Si j’arrive à voir les fixations métalliques d’un câble électrique à 4 km, je sais que mon instrument est prêt pour aller chasser les tempêtes sur Jupiter ou les divisions dans les anneaux de Saturne. La prochaine fois que vous verrez un pylône au loin, imaginez qu’il est aussi petit qu’une planète dans l’oculaire d’un télescope !